Model¶
[1]:
import torch_struct
import torch
import matplotlib.pyplot as plt
import matplotlib
[2]:
matplotlib.rcParams['figure.figsize'] = (7.0, 7.0)
Chain¶
- class torch_struct.LinearChainCRF(log_potentials, lengths=None, args={}, validate_args=False)[source]¶
Represents structured linear-chain CRFs with C classes.
For reference see:
An introduction to conditional random fields [SM+12]
Example application:
Bidirectional LSTM-CRF Models for Sequence Tagging [HXY15]
Event shape is of the form:
- Parameters
log_potentials (tensor) – event shape ((N-1) x C x C) e.g. \(\phi(n, z_{n+1}, z_{n})\)
lengths (long tensor) – batch_shape integers for length masking.
Compact representation: N long tensor in [0, …, C-1]
Implementation uses linear-scan, forward-pass only.
Parallel Time: \(O(\log(N))\) parallel merges.
Forward Memory: \(O(N \log(N) C^2)\)
[3]:
batch, N, C = 3, 7, 2
def show_chain(chain):
plt.imshow(chain.detach().sum(-1).transpose(0, 1))
# batch, N, z_n, z_n_1
log_potentials = torch.rand(batch, N, C, C)
dist = torch_struct.LinearChainCRF(log_potentials)
show_chain(dist.argmax[0])

[4]:
show_chain(dist.marginals[0])

[5]:
event = dist.to_event(torch.tensor([[0, 1, 0, 1, 1, 1, 0, 1]]), 2)
show_chain(event[0])

Hidden Markov Model¶
- class torch_struct.HMM(transition, emission, init, observations, lengths=None, validate_args=False)[source]¶
Represents hidden-markov smoothing with C hidden states.
Event shape is of the form:
- Parameters
transition (tensor) – log-probabilities (C X C) \(p(z_n| z_n-1)\)
emission (tensor) – log-probabilities (V x C) \(p(x_n| z_n)\)
init (tensor) – log-probabilities (C) \(p(z_1)\)
observations (long tensor) – indices (batch x N) between [0, V-1]
Compact representation: N long tensor in [0, …, C-1]
Implemented as a special case of linear chain CRF.
[6]:
batch, V, N, C = 10, 3, 7, 2
transition = torch.rand(C, C).log_softmax(0)
emission = torch.rand(V, C).log_softmax(0)
init = torch.rand(C).log_softmax(0)
observations = torch.randint(0, V, size=(batch, N))
dist = torch_struct.HMM(transition, emission, init, observations)
show_chain(dist.argmax[0])

Semi-Markov¶
- class torch_struct.SemiMarkovCRF(log_potentials, lengths=None, args={}, validate_args=False)[source]¶
Represents a semi-markov or segmental CRF with C classes of max width K
Event shape is of the form:
- Parameters
log_potentials – event shape (N x K x C x C) e.g. \(\phi(n, k, z_{n+1}, z_{n})\)
lengths (long tensor) – batch shape integers for length masking.
Compact representation: N long tensor in [-1, 0, …, C-1]
Implementation uses linear-scan, forward-pass only.
Parallel Time: \(O(\log(N))\) parallel merges.
Forward Memory: \(O(N \log(N) C^2 K^2)\)
[7]:
batch, N, C, K = 3, 10, 2, 6
def show_sm(chain):
plt.imshow(chain.detach().sum(1).sum(-1).transpose(0, 1))
# batch, N, K, z_n, z_n_1
log_potentials = torch.rand(batch, N, K, C, C)
log_potentials[:, :, :3] = -1e9
dist = torch_struct.SemiMarkovCRF(log_potentials)
show_sm(dist.argmax[0])

[8]:
show_sm(dist.marginals[0])

[9]:
# Use -1 for segments.
event = dist.to_event(torch.tensor([[0, 1, -1, 1, -1, -1, 0, 1, 1, -1, -1]]), (2, 6))
show_sm(event[0])

Alignment¶
- class torch_struct.AlignmentCRF(log_potentials, local=False, lengths=None, max_gap=None, validate_args=False)[source]¶
Represents basic alignment algorithm, i.e. dynamic-time warping, Needleman-Wunsch, and Smith-Waterman.
Event shape is of the form:
- Parameters
log_potentials (tensor) –
- event_shape (N x M x 3), e.g.
\(\phi(i, j, op)\)
Ops are 0 -> j-1, 1->i-1,j-1, and 2->i-1
local (bool) – if true computes local alignment (Smith-Waterman), else Needleman-Wunsch
max_gap (int or None) – the maximum gap to allow in the dynamic program
lengths (long tensor) – batch shape integers for length masking.
Implementation uses convolution and linear-scan. Use max_gap for long sequences.
Parallel Time: \(O(\log (M + N))\) parallel merges.
Forward Memory: \(O((M+N)^2)\)
[10]:
batch, N, M = 3, 15, 20
def show_deps(tree):
plt.imshow(tree.detach())
log_potentials = torch.rand(batch, N, M, 3)
dist = torch_struct.AlignmentCRF(log_potentials)
show_deps(dist.argmax[0])

[11]:
show_deps(dist.marginals[0])

Dependency Tree¶
- class torch_struct.DependencyCRF(log_potentials, lengths=None, args={}, multiroot=True, validate_args=False)[source]¶
Represents a projective dependency CRF.
Reference:
Bilexical grammars and their cubic-time parsing algorithms [Eis00]
Event shape is of the form:
- Parameters
log_potentials (tensor) – event shape (N x N) head, child or (N x N x L) head, child, labels with arc scores with root scores on diagonal e.g. \(\phi(i, j)\) where \(\phi(i, i)\) is (root, i).
lengths (long tensor) – batch shape integers for length masking.
Compact representation: N long tensor in [0, .. N] (indexing is +1)
Implementation uses linear-scan, forward-pass only.
Parallel Time: \(O(N)\) parallel merges.
Forward Memory: \(O(N \log(N) C^2 K^2)\)
[12]:
batch, N, N = 3, 10, 10
def show_deps(tree):
plt.imshow(tree.detach())
log_potentials = torch.rand(batch, N, N)
dist = torch_struct.DependencyCRF(log_potentials)
show_deps(dist.argmax[0])

[13]:
show_deps(dist.marginals[0])
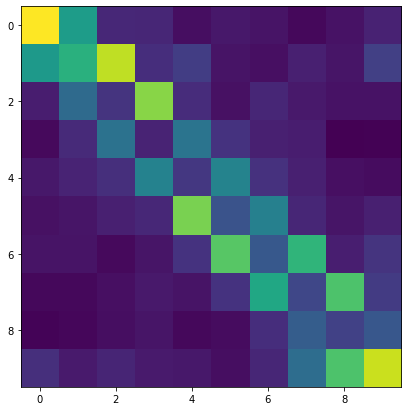
[14]:
# Convert from 1-index standard format. (Head is 0)
event = dist.to_event(torch.tensor([[2, 3, 4, 1, 0, 4]]), None)
show_deps(event[0])

Non-Projective Dependency Tree¶
- class torch_struct.NonProjectiveDependencyCRF(log_potentials, lengths=None, args={}, multiroot=False, validate_args=False)[source]¶
Represents a non-projective dependency CRF.
For references see:
Non-projective dependency parsing using spanning tree algorithms [MPRHajivc05]
Structured prediction models via the matrix-tree theorem [KGCPerezC07]
Event shape is of the form:
- Parameters
log_potentials (tensor) – event shape (N x N) head, child with arc scores with root scores on diagonal e.g. \(\phi(i, j)\) where \(\phi(i, i)\) is (root, i).
Compact representation: N long tensor in [0, .. N] (indexing is +1)
Note: Does not currently implement argmax (Chiu-Liu) or sampling.
[15]:
batch, N, N = 3, 10, 10
def show_deps(tree):
plt.imshow(tree.detach())
log_potentials = torch.rand(batch, N, N)
dist = torch_struct.NonProjectiveDependencyCRF(log_potentials)
show_deps(dist.marginals[0])
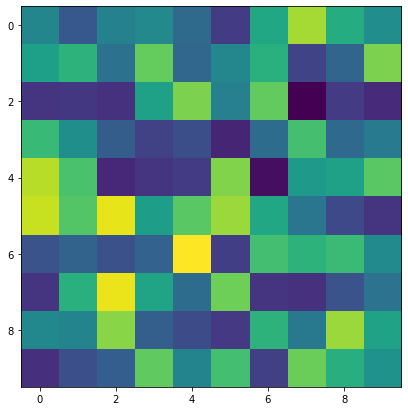
Binary Labeled Tree¶
- class torch_struct.TreeCRF(log_potentials, lengths=None, args={}, validate_args=False)[source]¶
Represents a 0th-order span parser with NT nonterminals. Implemented using a fast CKY algorithm.
For example usage see:
A Minimal Span-Based Neural Constituency Parser [SAK17]
Event shape is of the form:
- Parameters
log_potentials (tensor) – event_shape (N x N x NT), e.g. \(\phi(i, j, nt)\)
lengths (long tensor) – batch shape integers for length masking.
Implementation uses width-batched, forward-pass only
Parallel Time: \(O(N)\) parallel merges.
Forward Memory: \(O(N^2)\)
Compact representation: N x N x NT long tensor (Same)
[16]:
batch, N, NT = 3, 20, 3
def show_tree(tree):
t = tree.detach()
plt.imshow(t[ :, : , 0] +
2 * t[ :,:, 1] +
3 * t[ :,:, 2])
log_potentials = torch.rand(batch, N, N, NT)
dist = torch_struct.TreeCRF(log_potentials)
show_tree(dist.argmax[0])
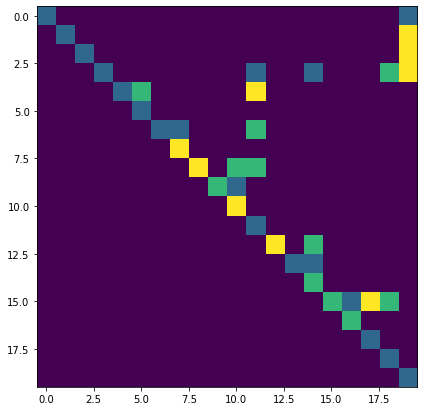
[17]:
show_tree(dist.marginals[0])
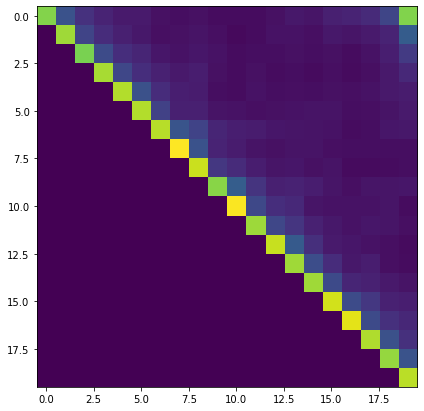
Probabilistic Context-Free Grammar¶
- class torch_struct.SentCFG(log_potentials, lengths=None, validate_args=False)[source]¶
Represents a full generative context-free grammar with non-terminals NT and terminals T.
Event shape is of the form:
- Parameters
log_potentials (tuple) – event tuple with event shapes terms (N x T) rules (NT x (NT+T) x (NT+T)) root (NT)
lengths (long tensor) – batch shape integers for length masking.
Implementation uses width-batched, forward-pass only
Parallel Time: \(O(N)\) parallel merges.
Forward Memory: \(O(N^2 (NT+T))\)
Compact representation: (N x N x NT) long tensor
[18]:
batch, N, NT, T = 3, 20, 3, 3
def show_prob_tree(tree):
t = tree.detach().sum(-1).sum(-1)
plt.imshow(t[ :, : , 0] +
2 * t[ :,:, 1] +
3 * t[ :,:, 2])
terminals = torch.rand(batch, N, T)
rules = torch.rand(batch, NT, NT+T, NT+T)
init = torch.rand(batch, NT).log_softmax(-1)
dist = torch_struct.SentCFG((terminals, rules, init))
term, rules, init = dist.argmax
[19]:
# Rules
show_prob_tree(rules[0])

[20]:
# Terminals
plt.imshow(term[:1])
[20]:
<matplotlib.image.AxesImage at 0x7f1877a1fb70>

Autoregressive / Beam Search¶
- class torch_struct.Autoregressive(model, initial_state, n_classes, n_length, normalize=True, start_class=0, end_class=None)[source]¶
Autoregressive sequence model utilizing beam search.
batch_shape -> Given by initializer
event_shape -> N x T sequence of choices
- Parameters
model (AutoregressiveModel) – A lazily computed autoregressive model.
init (tuple of tensors, batch_shape x …) – initial state of autoregressive model.
n_classes (int) – number of classes in each time step
n_length (int) – max length of sequence
- beam_topk(K)[source]¶
Compute “top-k” using beam search
- Parameters
K – top-k
- Returns
paths (K x batch x N x C)
- greedy_max()[source]¶
Compute “argmax” using greedy search.
- Returns
greedy_path (batch x N x C) greedy_max (batch) logits (batch x N x C)
- greedy_tempmax(alpha)[source]¶
Compute differentiable scheduled sampling using greedy search.
Based on:
Differentiable Scheduled Sampling for Credit Assignment [GDBK17]
- Parameters
alpha – alpha param
- Returns
greedy_path (batch x N x C) greedy_max (batch) logits (batch x N x C)
- sample(sample_shape=torch.Size([]))[source]¶
Compute structured samples from the distribution \(z \sim p(z)\).
- Parameters
sample_shape (torch.Size) – number of samples
- Returns
samples (sample_shape x batch_shape x event_shape)
- sample_without_replacement(sample_shape=torch.Size([]))[source]¶
Compute sampling without replacement using Gumbel trick.
Based on:
- Stochastic Beams and Where to Find Them: The Gumbel-Top-k Trick for
Sampling Sequences Without Replacement [KvHW19]
- Parameters
sample_shape (torch.Size) – batch_size
- Returns
paths (K x batch x N x C)
[21]:
batch, N, C, H, layer = 3, 10, 4, 5, 1
init = (torch.rand(batch, layer, H),
torch.rand(batch, layer, H))
def t(a):
return [t.transpose(0, 1) for t in a]
def show_ar(chain):
plt.imshow(chain.detach().transpose(0, 1))
class RNN_AR(torch.nn.Module):
def __init__(self, sparse=True):
super().__init__()
self.sparse = sparse
self.rnn = torch.nn.RNN(H, H, batch_first=True)
self.proj = torch.nn.Linear(H, C)
if sparse:
self.embed = torch.nn.Embedding(C, H)
else:
self.embed = torch.nn.Linear(C, H)
def forward(self, inputs, state):
if not self.sparse and inputs.dim() == 2:
inputs = torch.nn.functional.one_hot(inputs, C).float()
inputs = self.embed(inputs)
out, state = self.rnn(inputs, t(state)[0])
out = self.proj(out)
return out, t((state,))
dist = torch_struct.Autoregressive(RNN_AR(), init, C, N)
[22]:
path, scores, _ = dist.greedy_max()
show_ar(path[0])
print(scores[0])
tensor(-11.7909, grad_fn=<SelectBackward>)

[23]:
dist.log_prob(path.unsqueeze(0))
[23]:
tensor([[-11.7909, -11.8150, -11.7972]], grad_fn=<ViewBackward>)
[24]:
out = dist.beam_topk(5)[:, 0]
for i in range(3):
show_ar(out[i])
plt.show()



[25]:
out = dist.sample((5,))[:, 0 ]
print(out.shape)
for i in range(3):
show_ar(out[i])
plt.show()
torch.Size([5, 10, 4])



[26]:
out = dist.sample_without_replacement((5,))[:, 0]
for i in range(3):
show_ar(out[i])
plt.show()



[27]:
dist = torch_struct.Autoregressive(RNN_AR(sparse=False), init, C, N)
_, _, logits = dist.greedy_tempmax(1.0)
show_ar(logits[0])
loss = logits[0:1, torch.arange(10), torch.zeros(10).long()]
loss.sum().backward()
Base Class¶
- class torch_struct.StructDistribution(log_potentials, lengths=None, args={}, validate_args=False)[source]¶
Base structured distribution class.
Dynamic distribution for length N of structures \(p(z)\).
Implemented based on gradient identities from:
Inside-outside and forward-backward algorithms are just backprop [Eis16]
Semiring Parsing [Goo99]
First-and second-order expectation semirings with applications to minimum-risk training on translation forests [LE09]
- Parameters
log_potentials (tensor, batch_shape x event_shape) – log-potentials \(\phi\)
lengths (long tensor, batch_shape) – integers for length masking
- property argmax¶
Compute an argmax for distribution \(\arg\max p(z)\).
- Returns
argmax (batch_shape x event_shape)
- property count¶
Compute the log-partition function.
- cross_entropy(other)[source]¶
Compute cross-entropy for distribution p(self) and q(other) \(H[p, q]\).
- Parameters
other – Comparison distribution
- Returns
cross entropy (batch_shape)
- property entropy¶
Compute entropy for distribution \(H[z]\).
- Returns
entropy (batch_shape)
- kl(other)[source]¶
Compute KL-divergence for distribution p(self) and q(other) \(KL[p || q] = H[p, q] - H[p]\).
- Parameters
other – Comparison distribution
- Returns
cross entropy (batch_shape)
- kmax(k)[source]¶
Compute the k-max for distribution \(k\max p(z)\).
- Parameters :
k : Number of solutions to return
- Returns
kmax (k x batch_shape)
- log_prob(value)[source]¶
Compute log probability over values \(p(z)\).
- Parameters
value (tensor) – One-hot events (sample_shape x batch_shape x event_shape)
- Returns
log_probs (sample_shape x batch_shape)
- property marginals¶
Compute marginals for distribution \(p(z_t)\).
Can be used in higher-order calculations, i.e.
- Returns
marginals (batch_shape x event_shape)
- property max¶
Compute an max for distribution \(\max p(z)\).
- Returns
max (batch_shape)
- property partition¶
Compute the log-partition function.
[28]:
batch, N, C = 3, 7, 2
# batch, N, z_n, z_n_1
log_potentials = torch.rand(batch, N, C, C)
dist = torch_struct.LinearChainCRF(log_potentials, lengths=torch.tensor([N-1, N, N+1]))
show_chain(dist.argmax[0])
plt.show()
show_chain(dist.argmax[1])


[29]:
show_chain(dist.marginals[0])
plt.show()
show_chain(dist.marginals[1])
[30]:
def show_samples(samples):
show_chain(samples[0, 0])
plt.show()
show_chain(samples[1, 0])
plt.show()
show_chain(samples[0, 1])
[31]:
show_samples(dist.sample((10,)))



[32]:
show_samples(dist.topk(10))



[33]:
# Enumerate
x,_ = dist.enumerate_support()
print(x.shape)
for i in range(10):
show_chain(x[i][0])
plt.show()
torch.Size([256, 3, 7, 2, 2])










[34]:
plt.imshow(dist.entropy.detach().unsqueeze(0))
[34]:
<matplotlib.image.AxesImage at 0x7f1877c52c18>
